
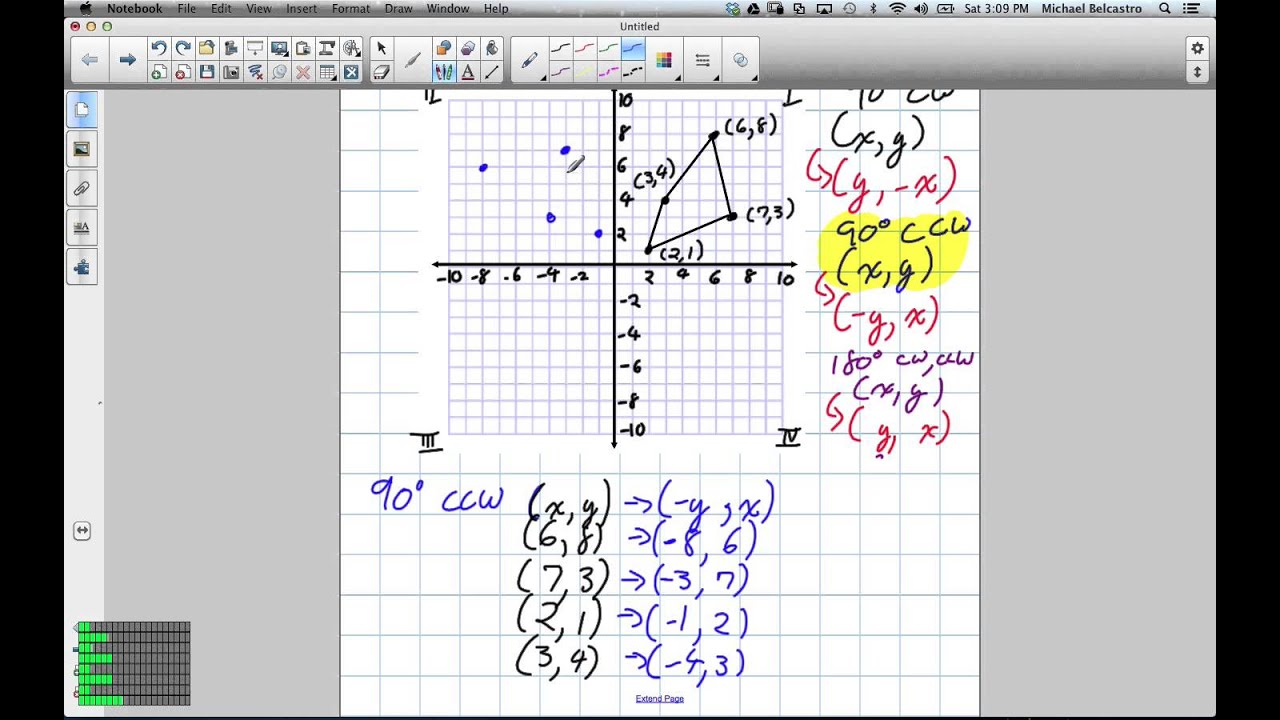
To use your example (1,10) becomes (10,-1). To rotate a two-dimensional shape around the origin 90 counterclockwise, we take the defining points of the shape, change the sign of the second coordinate. For multidimensional arrays, rot90 rotates in the plane formed by the first and second dimensions. The OP understands that if a point (x,y) becomes (y,-x) it is being rotated 90 deg clockwise about the origin. B rot90( A ) rotates array A counterclockwise by 90 degrees. The opposite is the case when we replace x with y and y with -x in the coordinates of a point - the result is a 90 deg clockwise rotation as shown by your example. x = y² i.e x = - y² This represents a sideways parabola which is concave to the left (a rotation of 90 deg anticlockwise). With regard to a point the rotation is 90 deg clockwise as you indicated in your post.Ĭonsider y = x² If we replace x with y and y with -x in the rule we get: With regard to a function this is a correct statement.

I can only assume you were not aware he was referring to the rule of a function when he said replacing x with y and y with -x produces a 90 deg anticlockwise rotation. I was wondering why you said the student was wrong? The student said “if you take a function y=f(x) and do the same thing i.e replace x with y and y with -x then the transformation is 90 deg anticlockwise.” When you look at the graph, you see that it is rotated 90 degrees clockwise from where it started.Ĭlick to expand.The OP understands that if a point (x,y) becomes (y,-x) it is being rotated 90 deg clockwise about the origin. However, since the sheet had already been flipped from the previous step, the final transformation becomes x' = y, y' = -x. This effectively exchanges the X and Y coordinates for each point on the graph: x' = y, y' = x. Next you flip the sheet over a second time by holding the bottom-left and top-right corners, such that they remain where they are but the top-left and bottom-right corners exchange positions. The new graph is effectively x' = -x, y' = y. When you have practiced this enough, you should be able to tell the 4 general rotations (90 degrees, 180 degrees, and 270 degrees) counterclockwise (positive direction), and thus their equivalents (270 degrees, 180 degrees, and 90 degrees) clockwise.
The vertical coordinates for all points on the graph remain unchanged. You begin by flipping the sheet over horizontally: everything on the left side of the graph moves to the right and everything on the right moves to the left. You manipulate the orientation of the sheet in order to transform the graph. There is a graph of some sort plotted on it as well.
Describe and graph rotational symmetry.In the video that follows, you’ll look at how to: rotate and click on a button next to it to rotate the page clockwise or counterclockwise.
90 degree rotation clockwise pdf#
The order of rotations is the number of times we can turn the object to create symmetry, and the magnitude of rotations is the angle in degree for each turn, as nicely stated by Math Bits Notebook. All kinds of PDF documents can be rotated online and for free. And when describing rotational symmetry, it is always helpful to identify the order of rotations and the magnitude of rotations.
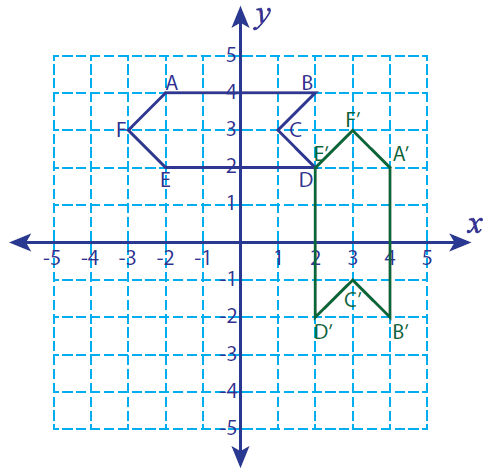
This means that if we turn an object 180° or less, the new image will look the same as the original preimage. Lastly, a figure in a plane has rotational symmetry if the figure can be mapped onto itself by a rotation of 180° or less.


 0 kommentar(er)
0 kommentar(er)
